В шахматных соревнованиях часто случается, что несыгранные партии приводят к различным нарушениям, таким как игрок, ожидающий своего соперника, который не является на партию, невыполнение норм для получения званий, изменение дополнительных показателей и, как следствие, распределения призовых мест, и т.д.

В попытке минимизировать эти нежелательные последствия, ФИДЕ Handbook (Российские Правила вида спорта «шахматы» предусматривают тоже – прим. переводчика) предусматривают, как действовать в каждом конкретном случае. Например, в круговых турнирах решение в подобной ситуации принимается в зависимости от того, сыграл ли выбывший (исключенный из турнира) игрок 50% от общего количества туров.

В этой статье мы будем говорить о турнирах, проводимых по Швейцарской системе, и дополнительных показателях, в которых «виртуальные соперники» «принимают участие». Это коэффициенты Бухгольца (сумма очков каждого соперника игрока) и Зонненборна-Бергера (сумма очков, набранных соперниками, у которых игрок выиграл, и половины очков, набранных соперниками, с которыми он сыграл вничью).

Во избежание путаницы, мы будем говорить только о системе Бухгольца.

Вычисление коэффициента «виртуального соперника» по системе Зонненборна-Бергера – это очень похожий процесс. (Примечание: виртуального соперника можно также применить в дополнительном показателе коэффициент Прогресса, но ФИДЕ больше не рекомендует использование этого коэффициента, поэтому мы не будем это обсуждать)

Прежде всего, давайте посмотрим на соответствующие статьи в ФИДЕ Handbook.

Статья C.02 13.15.2: Для подсчета дополнительных показателей игрок, соперник которого не явился на партию, будет считаться сыгравшим партию с виртуальным соперником с равным количеством очков перед туром, все дальнейшие партии которого должны считаться завершившимися в ничью. Результат в самом туре, полученный без игры, будет рассматриваться как обычный результат.

Это дает нам формулу:

Svon= SPR + (1-SfPR) + 0,5*(n-R), где для игрока P, который не играл в туре R:

• n = количество завершенных туров
• Svon = количество очков виртуального соперника после тура n
• SPR = количество очков игрока P перед туром R
• SfPR = результат без игры игрока P в туре R

Статья C.02 13.15.3: Для подсчета дополнительного коэффициента все несыгранные партии, в которые косвенно вовлечены игроки (результаты получены из-за неявки соперников), считаются закончившимися вничью.

В нашем первом примере игрок X не явился на первый из 7 туров и, в конце концов, был исключен из оставшихся туров. Игрок A – это соперник, который получил очко без игры. После 7-ми туров игрок A имеет коэффициент Бухгольца, равный 28.5 от игроков, у которых не было несыгранных партий. Но какой будет его коэффициент Бухгольца от встречи с игроком в первом туре? 0 очков?

Нет, это будет абсолютно несправедливо. Мы будем считать, что в первом туре игрок А встретился с виртуальным соперником.

У этого «виртуального соперника» было 0 очков до начала турнира, и он сыграл вничью во всех оставшихся турах (за исключением первого тура, в котором он получил поражение без игры).

Таким образом, после 7-ми туров, у него будет 3 очка. Действительно, согласно формуле

Svon= 0+ (1-1) + 0, 5*(7-1) =3

Итак, коэффициент Бухгольца игрока A будет равен 28.5+3=31.5

Во втором примере мы рассмотрим игрока B, который встретился с игроком A во втором туре. В конце турнира сумма очков соперников игрока B равна 26.5. Будет ли это его коэффициентом Бухгольца?

Нет, потому что один из его соперников (игрок А) имел несыгранную партию, которая теперь считается сыгранной вничью (Статья C.02 13.15.3). Таким образом, коэффициент Бухгольца игрока B будет равен 26.

В нашем последнем примере игрок С начал с результатом 3 из 3, не играл в четвертом туре, но играл во всех остальных турах. Его коэффициент от реальных соперников равен 25.5

Количество очков его «виртуального соперника» в четвертом туре равно:

Svon= 3 + (1-0) + 0.5*(7-4) =5.5

поэтому его коэффициент Бухгольца равен 25.5+5.5=31

Мы надеемся, что это статья помогла пролить немного света на эту запутанную тему.

Более детальное разъяснение, написанное международным арбитром профессором Р. Анатарамом, может быть найдено читателями на сайте ФИДЕ.

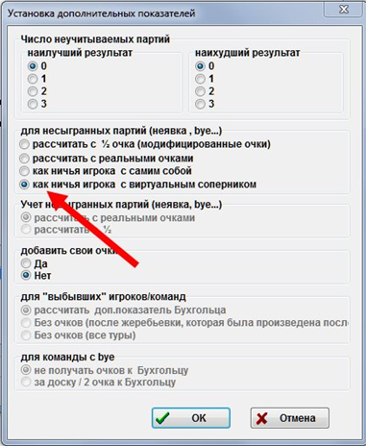
Примечание: для пользователей программы жеребьевки Swiss-Manager параметр «виртуального соперника» установлен по умолчанию (см. фото – прим. переводчика). Если Положение турнира предусматривает другую опцию, то необходимо изменить параметры в ручном режиме